Comprendre les algorithmes de parcours en 8 minutes

Les algorithmes de parcours de graphe sont beaucoup plus simples qu’ils en ont en l’air. Et ils tombent fréquemment en entretien d’embauche. En quelques minutes, on va se mettre à jour sur ces algorithmes fondamentaux !

Une histoire de connexion

Du DOM de cette page aux réseaux des Internets en passant par les liens qui t’ont emmenés dans mon humble demeure, tout est représenté par des graphes. Tout est une histoire de connexion. Tout est lié. Et le truc à comprendre tout de suite c’est qu’à partir du moment où il y a des connexions, ça peut être représenté par un graphe !

L’objectif de l’article d’aujourd’hui c’est de comprendre comment utiliser ces liens et les parcourir dans un graphe. Et même si ça ne te servira pas tous les jours dans ton boulot, ça va te servir à un moment décisif.

Imagine, t’es en entretien d’embauche et comme souvent au début, ça se passe très bien. On te pose des questions sur Python, Javascript et Git et t’enchaînes les réponses comme un pro. On te met alors devant un PC et on te pose une question à laquelle tu t’attendais pas.

---

La matrice d’adjacence ci-dessous représente un labyrinthe que nous voulons explorer. Avec les coordonnées de départ en paramètre d’entrée, écrivez un algorithme qui permet de le parcourir entièrement.

matrix = [
            [0,1,1,0,0],
            [1,1,0,0,0],
            [1,0,0,1,0],
            [1,1,0,1,1],
            [0,1,0,0,0]
          ]
start = (0,4)

• 0 représente un chemin ouvert qui peut être parcouru et traversé.
• 1 représente un chemin fermé qui ne peut être parcouru ou traversé.

Remplacer par un X les chemins qu’il est possible de parcourir depuis le point de départ, puis afficher le labyrinthe. Vous pouvez assumer que le point de départ sera toujours un chemin ouvert. Vous avez 25 minutes.

---

Si t’as aucune notion de structure de données linéaires ou non-linéaires : c’est mission impossible. Mais même avec tout ça, c’est pas gagné. Car cette question sert au recruteur à vérifier une seule chose.

Est-ce que tu connais un des algorithmes fondamentaux de parcours de graphe ?

Parcours en profondeur (Depth First Search)

L’algorithme de parcours en profondeur (DFS) fait partie de ces algorithmes fondamentaux. Il est utilisé pour parcourir entièrement, en profondeur, un graphe. Je répète, c’est important de comprendre que le DFS est un algorithme qui explore en profondeur.

Il choisit un chemin, va au bout de ce chemin, puis revient sur ses pas et fait pareil pour tous les chemins possibles dans le graphe donné. C’est toujours plus clair avec une animation pompée sur les Internets.

L’objectif du DFS est de faire des recherches complètes ou bien du retour sur trace (backtracking). Un chemin à la fois, il va explorer dans les moindres recoins le chemin actuel. Puis il va passer au chemin suivant pour être sûr d’épuiser toutes les possibilités par chemin. Je te répète 50 fois la même chose car c’est important que tu imprimes ce concept de profondeur tout de suite.

Le DFS base son fonctionnement sur une structure de données qu’on a vue auparavant : la stack. En tous cas, dans la forme itérative de l’algorithme. Ça peut être fait sous forme récursive (la récursion faisant en fait office de stack) mais on va rester le plus simple possible aujourd’hui.

Je vais te montrer ma solution au problème du labyrinthe avec un DFS. Pour que ça soit le plus accessible possible, chaque étape de l’algorithme est commentée avec un numéro dans le code. Chaque numéro correspond à une explication de code juste après. N’hésite pas à lire le code et les explications en même temps, ça sera plus simple.

Python (3.6.9)

from collections import deque 

class Graph():
    def __init__(self, adjacency_matrix):
        self.adjacency_matrix = adjacency_matrix


    def display(self):
        for row in self.adjacency_matrix:
            display_row = ''
            for value in row:
                display_row += str(value) + ' '
            print(display_row)


    def depth_first_search(self, start):
        stack = deque() # 1
        deja_vu = list() # 1

        stack.appendleft(start) # 2

        while stack: # 3
            current_node_row, current_node_column = stack.popleft() # 4

            self.adjacency_matrix[current_node_row][current_node_column] = 'X' # 5

            deja_vu.append((current_node_row, current_node_column))  # 6

            for valid_adjacent_node in self.valid_adjacent_nodes((current_node_row, current_node_column), deja_vu): # 7
                stack.appendleft(valid_adjacent_node) # 8


    def valid_adjacent_nodes(self, currentNode, deja_vu):
        # UP, DOWN, LEFT, RIGHT
        directions_offset = [(-1, 0), (1, 0), (0, -1), (0, 1)]
        current_node_row, current_node_column = currentNode

        # searching for valid node around the current node 
        # by updating coordinates at each iteration
        for row_offset, column_offset in directions_offset:
            next_row, next_col = (current_node_row + row_offset, current_node_column + column_offset)

            # if the node is valid and not already deja_vu 
            # we push it directly in the stack and continue
            if self.is_valid_node(next_row, next_col) and (next_row, next_col) not in deja_vu:
                yield (next_row, next_col)


    def is_valid_node(self, row, column):
        # to be valid a node need to be
        # - inbound of the limit of the matrix
        # - equal to 0
        if column >= 0 and row >= 0 and column < len(self.adjacency_matrix) and row < len(self.adjacency_matrix) and self.adjacency_matrix[row][column] == 0:
            return True
        return False


myGraph = Graph([
            [0,1,1,0,0],
            [1,1,0,0,0],
            [1,0,0,1,0],
            [1,1,0,1,1],
            [0,1,0,0,0]
          ])

print('Initial maze')
myGraph.display()

myGraph.depth_first_search((0,4))

print('\nMaze after DFS')
myGraph.display()

# Initial maze
# 0 1 1 0 0 
# 1 1 0 0 0 
# 1 0 0 1 0 
# 1 1 0 1 1 
# 0 1 0 0 0 

# Maze after DFS
# 0 1 1 X X 
# 1 1 X X X 
# 1 X X 1 X 
# 1 1 X 1 1 
# 0 1 X X X 

Test et joue avec le code en live ici ! –> https://repl.it/@jesuisundev/DFS

• 1 : On initialise une stack et un tableau vide.

La stack va être empilée et dépilée tout au long du processus. On veut une stack car c’est son fonctionnement LIFO qui va nous permettre de toujours aller plus profond dans le labyrinthe. Encore une fois, je te soûle avec cette notion de profondeur car c’est important.

Le tableau va nous permettre de se rappeler sur quel chemin on est déjà passé pour être sûr de jamais repasser deux fois au même endroit.

• 2 : On empile le point de départ dans la stack

Au début, le point de départ est le paramètre d’entrée. Puis, à chaque itération, ça va être le chemin au sommet de la stack -> le plus profond trouvé!

• 3 : Tant que la stack n’est pas vide, on itère sur chacun des chemins de la même façon

C’est dans ce while que l’algorithme va travailler. La fin de cette boucle signifie la résolution du problème.

• 4 : On dépile du sommet de la stack le chemin sur lequel on va travailler cette itération
• 5 : Ici, on fait ce qu’il faut pour régler le problème donné. C’est ici que la logique métier devrait apparaître.

Dans notre cas, on a juste à mettre un X dans la case. Easy!

• 6 : On a fini le travail avec ce chemin, on peut le mettre dans le tableau de déjà vu pour ne plus passer dessus dans l’avenir
• 7 : On va chercher tous les chemins adjacents au chemin courant. On va pousser seulement ceux qui sont valides dans la stack

Pour chercher les chemins adjacents, on va simplement regarder les chemins autour du chemin courant. On le fait dans un ordre arbitraire, peu importe, (ici haut, bas, gauche, droite) en changeant les coordonnées du chemin.

Les chemins valides pour un parcours doivent être dans les limites de la matrice d’adjacence et contenir la valeur 0.

Et c’est tout ! On a plus qu’à tourner sur notre stack jusqu’à qu’elle soit vide et afficher le labyrinthe. Problème réglé, labyrinthe parcouru. Tu peux faire le fifou, à toi le job !

Comme image mentale tu peux imaginer le DFS comme un serpent. Un serpent qui va toujours essayer d’aller dans les moindres recoins d’un graphe. Tu as une belle animation d’un DFS sur le wiki.

À ce moment-là, t’es fier de toi. Tu crois que l’entretien est fini et t’est déjà entrain de ranger tes affaires de façon nonchalante. Sauf que le recruteur en question décide de te faire un double tacle à la gorge ! Il te pose un second problème sur la table.

---

En reprenant le même contexte que précédemment, nous souhaitons désormais savoir si un chemin existe entre deux points. Avec les coordonnées de départ et les coordonnées de la cible en paramètres, écrivez un algorithme qui renvoie True si un chemin existe entre les deux chemins, False sinon.

matrix = [
            [0,1,1,0,0],
            [1,1,0,0,0],
            [1,0,0,1,0],
            [1,1,0,1,1],
            [0,1,0,0,0]
          ]
start = (0,4)
target = (4, 4)

• 0 représente un chemin ouvert qui peut être parcouru et traversé.
• 1 représente un chemin fermé qui ne peut être parcouru ou traversé.

Vous pouvez assumer que le point de départ sera toujours un chemin ouvert. Vous avez 25 minutes.

---

Oui, tu peux tout à fait résoudre le problème avec un DFS. Mais c’est pas ça que le recruteur veut que tu lui fasses. Il y a un algorithme plus optimisé pour cette question spécifiquement.

Parcours en largeur (Breadth First Search)

L’algorithme de parcours en largeur (BFS) est le second algorithme fondamental de parcours. Il est utilisé pour explorer un graphe rapidement dans la largeur, couche par couche, niveau par niveau. Chaque itération va augmenter la distance par rapport au nœud de départ.

Un des objectifs avec le BFS est de déterminer rapidement si un chemin existe entre deux points. Il peut aussi déterminer le nombre de niveaux qui sépare ces deux points. Cet algorithme va explorer, niveau par niveau dans tous les chemins en même temps, au lieu de se concentrer profondément chemin par chemin comme le DFS.

Le BFS base aussi son fonctionnement sur une structure de données qu’on a vue auparavant : la queue. C’est fou, c’est comme si j’avais prévu l’ordre des articles. La façon de fonctionner de type FIFO de la queue va nous permettre de passer de niveau en niveau dans notre graphe.

Et j’ai une super bonne nouvelle. Tu connais déjà l’algorithme du BFS ! Oui ! Tu sais déjà parcourir un graphe en largeur. Tu as plus qu’à te lancer !

L’algorithme du parcours en largeur est le même que l’algorithme du parcours en profondeur ! On a juste à échanger les structures de données entre la stack et la queue et le tour est joué.

`Python (3.6.9)

from collections import deque 

class Graph():
    def __init__(self, adjacency_matrix):
        self.adjacency_matrix = adjacency_matrix


    def breadth_first_search(self, start, destination):
        queue = deque()
        deja_vu = list()

        queue.append(start)

        while queue:
            currentNodeRow, currentNodeColumn = queue.popleft()

            if destination == (currentNodeRow, currentNodeColumn):
                return True

            deja_vu.append((currentNodeRow, currentNodeColumn))

            for validAdjacentNode in self.validAdjacentNodes((currentNodeRow, currentNodeColumn), deja_vu):
                queue.append(validAdjacentNode)

        return False


    def validAdjacentNodes(self, currentNode, deja_vu):
        directions_offset = [(-1, 0), (1, 0), (0, -1), (0, 1)]
        currentNodeRow, currentNodeColumn = currentNode

        for row_offset, column_offset in directions_offset:
            next_row, next_col = (currentNodeRow + row_offset, currentNodeColumn + column_offset)

            if self.isValidNode(next_row, next_col) and (next_row, next_col) not in deja_vu:
                yield (next_row, next_col)


    def isValidNode(self, row, column):
        if column >= 0 and row >=0 and column < len(self.adjacency_matrix) and row < len(self.adjacency_matrix) and self.adjacency_matrix[row][column] == 0:
            return True
        return False


myGraph = Graph([
            [0,1,1,0,0],
            [1,1,0,0,0],
            [1,0,0,1,0],
            [1,1,0,1,1],
            [0,1,0,0,0]
          ])


start = (0, 4)
destination = (4, 4)
print(myGraph.breadth_first_search(start, destination))
# True

start = (0, 4)
destination = (4, 0)
print(myGraph.breadth_first_search(start, destination))
# False

start = (0, 4)
destination = (0, 0)
print(myGraph.breadth_first_search(start, destination))
# False

start = (4, 4)
destination = (2, 1)
print(myGraph.breadth_first_search(start, destination))
# True

Test et joue avec le code en live ici ! –> https://repl.it/@jesuisundev/BFS

Comme image mentale j’aime bien imaginer le BFS comme une onde de choc. Elle part d’un point et se propage, niveau par niveau, en couvrant toute la largeur du graphe. Aller une dernière animation pour bien ancrer tout ce qu’on vient de voir dans le cerveau !

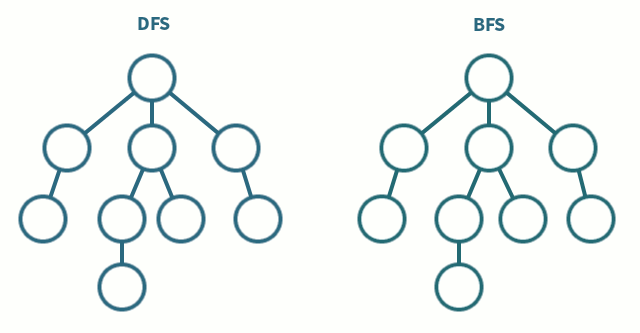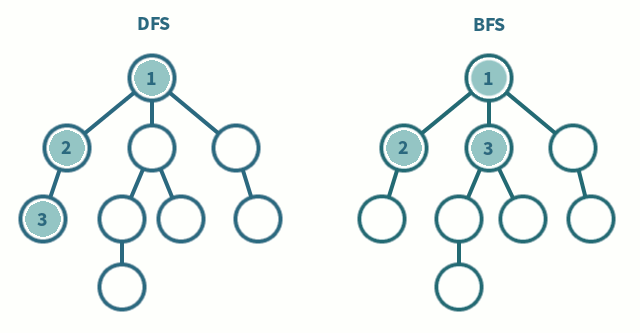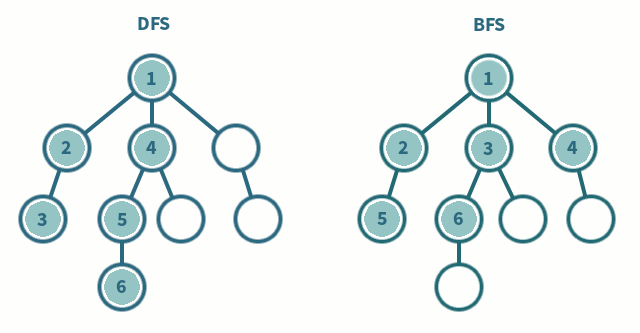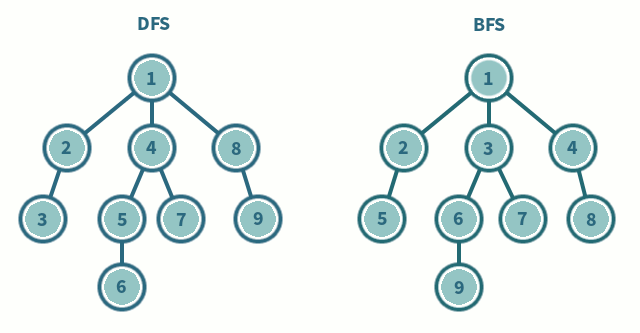
Ça y est, cette fois l’entretien est terminé ! Tu repars comme un champion et quelques jours plus tard, tu commences à négocier ton prochain salaire.

Épilogue

Si tu as saisi la logique du premier coup bravo ! Personnellement il m’a fallu du temps de compréhension et de pratique avant de pouvoir l’appliquer sur des cas réels. La meilleure vidéo que j’ai jamais vue pour une explication LIMPIDE c’est celle-là. Je te la conseille fortement. Sinon, y’a les cours du MIT (BFS, DFS) qui sont excellents aussi !